Função inversa

Em matemática, a função inversa de uma função ${\displaystyle f:X\rightarrow Y}$ é, quando existe, a função ${\displaystyle f^{-1}:Y\rightarrow X}$ tal que ${\displaystyle f\circ f^{-1}=\mathrm {id} _{X}}$ e ${\displaystyle f^{-1}\circ f=\mathrm {id} _{Y}}$ (id=função identidade). Ou seja, o que era domínio na função original (o conjunto ${\displaystyle X}$ neste caso, ilustrado na figura abaixo) vira imagem na função inversa, e o que era imagem na função original (${\displaystyle Y}$, neste caso - ilustrado na figura abaixo) vira domínio.

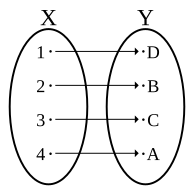
Uma função que tenha inversa diz-se invertível. Se uma função for invertível, então tem uma única inversa. Uma condição necessária e suficiente para que uma função seja invertível é que seja bijectiva^[1].

Se ${\displaystyle f:X\to Y}$ for uma função injectiva de ${\displaystyle X}$ em ${\displaystyle Y}$, então ${\displaystyle f}$ é também uma função bijectiva de ${\displaystyle X}$ em ${\displaystyle f(X)}$. Consequentemente, tem uma inversa de ${\displaystyle f(X)}$ em ${\displaystyle X}$. Por abuso de linguagem, também se designa esta função por inversa de ${\displaystyle f}$, embora o seu domínio não seja, em geral, o conjunto ${\displaystyle Y}$.

Seja ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ uma função bijetiva definida por ${\displaystyle y=f(x)}$. Resolvendo ${\displaystyle y=f(x)}$ para ${\displaystyle x}$ em função de ${\displaystyle y}$, temos determinado uma função ${\displaystyle x=g(y)}$. Esta função é a função inversa de ${\displaystyle f}$, i.e. ${\displaystyle g=f^{-1}}$.^[2]

Exemplo:

Para determinarmos a inversa da função ${\displaystyle f(x)=x+1}$ podemos proceder da seguinte forma:

1. ${\displaystyle f(x)=x+1}$
2. ${\displaystyle y=x+1}$
3. ${\displaystyle x=y+1}$
4. ${\displaystyle y=x-1}$
5. Portanto, ${\displaystyle f^{-1}(x)=x-1}$

Dadas as funções ${\displaystyle f:A\to B}$ e ${\displaystyle g:B\to A}$, diremos que ${\displaystyle g}$ é função inversa à esquerda de ${\displaystyle f}$quando a função composta ${\displaystyle g\circ f=id_{A}:A\to A}$ (id=função identidade), ou seja, quando ${\displaystyle g(f(x))=x}$ para todo ${\displaystyle x}$ pertencente ao conjunto A. Uma função ${\displaystyle f}$ possui inversa à esquerda se, e somente se, for injectiva.^[3] . Por exemplo, a função ${\displaystyle f:\mathbb {N} \to \mathbb {R} }$ dada por ${\displaystyle f(x)=2x}$, que é injetiva e não sobrejetiva, tem como inversa ${\displaystyle g(x)={\frac {x}{2}}}$, porque a função composta ${\displaystyle (g\circ f)(x)=g(f(x))={\frac {2x}{2}}=x}$ para todo ${\displaystyle x\in \mathbb {N} }$, a qual é a função identidade.

Dadas as funções g:B→A e f:A→B e , diremos que g é uma inversa à direita de f quando a função composta f O g = idB:B→B, ou seja, quando f(g(x)) = x para todo y pertencente ao conjunto B. Uma função f possui inversa à direita se, e somente se, for sobrejetiva.^[3]

Referências

Outros projetos Wikimedia também contêm material sobre este tema:
	Livros e manuais no Wikilivros