NURBS
No artigo de hoje falaremos sobre NURBS, tema que tem se tornado cada vez mais relevante nos últimos anos. NURBS tornou-se um ponto de interesse para muitas pessoas, seja pelo seu impacto na sociedade, pela sua relevância histórica ou pela sua influência na cultura popular. Ao longo deste artigo iremos explorar diferentes aspectos relacionados com NURBS, desde a sua origem e evolução, até à sua projeção atual e futura. Descobriremos sua importância na vida das pessoas e como ela vem estabelecendo padrões em diversas áreas. Sem dúvida, NURBS é um tema que gera grande interesse e com o qual podemos aprender muito.
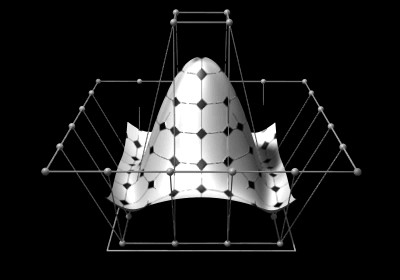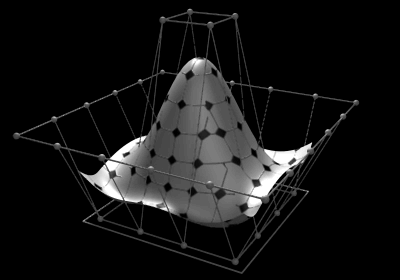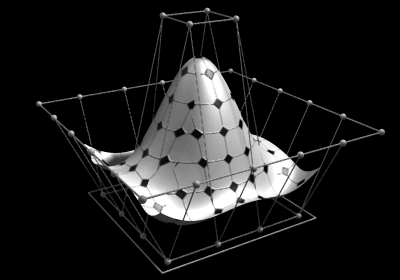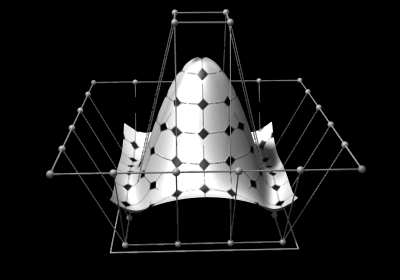

Versão animada
Non Uniform Rational Basis Spline (NURBS) é um modelo matemático usado regularmente em programas gráficos para gerar e representar curvas e superficies.
História

O desenvolvimento do NURBS (Non Uniform Rational Basis Spline) começou na década de 50 por engenheiros que precisavam de uma representação matemática para superfícies livres como as que são usadas nos chassis dos automóveis, que poderiam ser reproduzidas quando se quisesse. Representações anteriores desse tipo de superfícies apenas existiam como um modelo único criado por um designer.
Os pioneiros neste tipo de desenvolvimento foram Pierre Bézier que trabalhou como engenheiro da Renault, e Paul de Casteljau que trabalhou na Citroën, ambos na França. Bézier trabalhou quase paralelamente a Casteljau, ambos sabiam um do trabalho do outro. Mas como Bézier publicou os resultados do seu trabalho, os usuários frequentes desses softwares para desenhar curvas — que são representadas com controle dos pontos fora da sua curva- a conhecem como curva de Bézier, enquanto as de Casteljau´s apenas são conhecidas e utilizadas em algoritmos que ele desenvolveu para as superficies paramétricas. Na década de 60 tornou-se claro que as Uniform Space|Non-Uniform, rational B-splines são uma generalização das curvas de Bézier, que podem ser consideradas como curvas uniformes, não racionais básicas.
No início, NURBS foram apenas utilizadas em pacotes de CAD para empresas automotivas. Mais tarde elas tornaram-se parte de pacotes de programas gráficos
Em tempo real, a interpretação interativa das curvas e superfícies NURBS só estiveram disponíveis em workstations em 1989. Em 1993, a primeira NURBS interativa para PCs, chamadas NöRBS, foi desenvolvida por CAS Berlim, uma pequena empresa cooperando com a Universidade Técnica de Berlim. Hoje em dia, a maioria dos computadores gráficos disponibilizam tecnologia NURBS.
Uso

A tecnologia NURBS está quase omnipresente para CAD na engenharia e na maioria da industria é usado em grande parte como tecnologia standard.
Isto permite representação de formas geométricas de uma forma compacta. Elas podem ser eficientemente moldadas por programas de computador e ainda permitem uma fácil interacção com o utilizador. Superficies NURBS são funções de dois parametros mapeados para uma superficie tridimensional. Esta forma da superfície é determinada por pontos de controlo.
De uma forma geral, podemos dizer que editar curvas e superfícies NURBS é altamente intuitivo e previsivel. Os pontos de controlo são sempre connectados directamente à curva/superficie, ou agem como se estivessem connectadas.
A superficie em construção, por exemplo um motor de um yacht, é normalmente composto por várias superficies NURBS conhecidas como as patches. Estas patches devem estar todas juntas de maneira a que as fronteiras sejam invisiveis.
A continuação geométrica faz com que a forma resulte numa superfície; desde que as superficies NURBS sejam funções, isto possibilita também discutir as derivadas das superficies no que respeita às paramétricas. Isto é conhecido como paramétricas continuadas. A parametrização continuada de um determinado grau implica uma continuidade nesse grau.
Exemplo: um círculo
Enquanto as curvas não racionais não são suficientes para representar um círculo, isto é um dos muitos passos de controlo das curvas NURBS que podemos parametrizar uniformemente o círculo num plano xy:
| x | y | z | weight |
|---|---|---|---|
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 |
| −1 | 1 | 0 | |
| −1 | 0 | 0 | 1 |
| −1 | −1 | 0 | |
| 0 | −1 | 0 | 1 |
| 1 | −1 | 0 | |
| 1 | 0 | 0 | 1 |
Veja também
Referências
- Les Piegl & Wayne Tiller: The NURBS Book, Springer-Verlag 1995–1997 (2nd ed.). Principal referência para Bézier, B-Spline e NURBS; capítulos sobre representação matemática e construção de curvas e superfícies, interpolação, modificação de formas e conceitos de programação.
- Dr. Thomas Sederberg, BYU NURBS (PDF).
- Dr. Lyle Ramshaw. Blossoming: A connect-the-dots approach to splines, Research Report 19, Compaq Systems Research Center, Palo Alto, CA, June 1987
- David F. Roger: An Introduction to NURBS with Historical Perspective, Morgan Kaufmann Publishers 2001. Bom livro introdutório sobre NURBS e assuntos correlatos.
- Foley, van Dam, Feiner & Hughes: Computer Graphics Principles and Practice, Addison Wesley 1996 (2nd ed.).
Ligações externas
- About Nonuniform Rational B-Splines - NURBS
- An Interactive Introduction to Splines
- NURBS with 3ds max tutorials (en)
- http://www.cs.bris.ac.uk/Teaching/Resources/COMS30115/all_9.pdf
- http://devworld.apple.com/dev/techsupport/develop/issue25/schneider.html
- http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/AV0405/DONAVANIK/bezier.html
- http://mathcs.holycross.edu/~croyden/csci343/notes/Lecture33_CurvesIII.ppt
- http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/notes.html
