Teste da condensação de Cauchy
Aspeto mover para a barra lateral ocultarEm matemática, o teste da condensação de Cauchy é um teste padrão de convergência para séries infinitas. Seja uma seqüência não-negativa e monotonicamente decrescente f ( n ) {\displaystyle f(n)} de números reais, então a série ∑ n = 1 ∞ f ( n ) {\displaystyle \textstyle \sum _{n=1}^{\infty }f(n)} converge se e somente se a "série condensada" ∑ n = 0 ∞ 2 n f ( 2 n ) {\displaystyle \textstyle \sum _{n=0}^{\infty }2^{n}f(2^{n})} converge. Ademais, se essas séries convergem, a soma da série condensada não é maior do que 2 ∑ n = 1 ∞ f ( n ) {\displaystyle 2\textstyle \sum _{n=1}^{\infty }f(n)} .
de 
converge se e somente se a "série condensada"
∑
n
=
0
∞
2
n
f
(
2
n
)
{\displaystyle \textstyle \sum _{n=0}^{\infty }2^{n}f(2^{n})}
converge. Ademais, se essas séries convergem, a soma da série condensada não é maior do que
2
∑
n
=
1
∞
f
(
n
)
{\displaystyle 2\textstyle \sum _{n=1}^{\infty }f(n)}
.
Este teste é bastante técnico, assim como o teste de convergência de Abel, e seu principal objetivo é mostrar a convergência das p-séries quando p > 1 {\displaystyle p>1} .
.
Estimativas e demonstração
O teste da condensação de Cauchy segue das seguintes estimativas:
0 ≤ ∑ n = 1 ∞ f ( n ) ≤ ∑ n = 0 ∞ 2 n f ( 2 n ) ≤ 2 ∑ n = 1 ∞ f ( n ) ≤ + ∞ {\displaystyle 0\ \leq \ \sum _{n=1}^{\infty }f(n)\ \leq \ \sum _{n=0}^{\infty }2^{n}f(2^{n})\ \leq \ 2\sum _{n=1}^{\infty }f(n)\ \leq \ +\infty }
as quais devem ser entendidas como desigualdades nos números reais estendidos.
Para se chegar a primeira desigualdade os termos são reassociados em grupos com número de elementos sendo potências de dois, e depois, em cada grupo, substitui-se seus termos pelo primeiro - que é o maior deles -, já que eles formam uma seqüência não-crescente.
∑ n = 1 ∞ f ( n ) = f ( 1 ) + f ( 2 ) + f ( 3 ) + f ( 4 ) + f ( 5 ) + f ( 6 ) + f ( 7 ) + ⋯ = f ( 1 ) + ( f ( 2 ) + f ( 3 ) ) + ( f ( 4 ) + f ( 5 ) + f ( 6 ) + f ( 7 ) ) + ⋯ ≤ f ( 1 ) + ( f ( 2 ) + f ( 2 ) ) + ( f ( 4 ) + f ( 4 ) + f ( 4 ) + f ( 4 ) ) + ⋯ = f ( 1 ) + 2 f ( 2 ) + 4 f ( 4 ) + ⋯ = ∑ n = 0 ∞ 2 n f ( 2 n ) {\displaystyle {\begin{array}{rcccccccl}\sum _{n=1}^{\infty }f(n)&=&f(1)&+&f(2)+f(3)&+&f(4)+f(5)+f(6)+f(7)&+&\cdots \\&=&f(1)&+&{\Big (}f(2)+f(3){\Big )}&+&{\Big (}f(4)+f(5)+f(6)+f(7){\Big )}&+&\cdots \\&\leq &f(1)&+&{\Big (}f(2)+f(2){\Big )}&+&{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}&+&\cdots \\&=&f(1)&+&2f(2)&+&4f(4)&+&\cdots =\sum _{n=0}^{\infty }2^{n}f(2^{n})\end{array}}}
Para se chegar a segunda desigualdade, os termos da série são novamente reassociadas em grupos com número de elementos sendo potências de dois, onde em cada grupo é tomada, novamente, uma substituição por um termo maior na série não-crescente f ( n ) {\displaystyle f(n)} .
∑ n = 0 ∞ 2 n f ( 2 n ) = f ( 1 ) + ( f ( 2 ) + f ( 2 ) ) + ( f ( 4 ) + f ( 4 ) + f ( 4 ) + f ( 4 ) ) + ⋯ = ( f ( 1 ) + f ( 2 ) ) + ( f ( 2 ) + f ( 4 ) + f ( 4 ) + f ( 4 ) ) + ⋯ ≤ ( f ( 1 ) + f ( 1 ) ) + ( f ( 2 ) + f ( 2 ) + f ( 3 ) + f ( 3 ) ) + ⋯ = 2 ∑ n = 1 ∞ f ( n ) {\displaystyle {\begin{array}{rcl}\sum _{n=0}^{\infty }2^{n}f(2^{n})&=&f(1)+{\Big (}f(2)+f(2){\Big )}+{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}+\cdots \\&=&{\Big (}f(1)+f(2){\Big )}+{\Big (}f(2)+f(4)+f(4)+f(4){\Big )}+\cdots \\&\leq &{\Big (}f(1)+f(1){\Big )}+{\Big (}f(2)+f(2)+f(3)+f(3){\Big )}+\cdots =2\sum _{n=1}^{\infty }f(n)\end{array}}}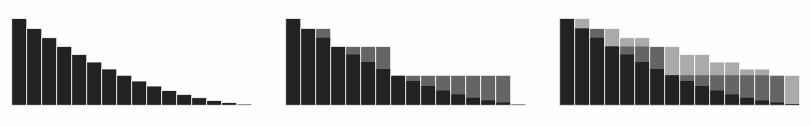
Visualização do argumento: somas parciais das séries
∑
f
(
n
)
{\displaystyle \textstyle \sum f(n)}
,
∑
2
n
f
(
2
n
)
{\displaystyle \sum 2^{n}f(2^{n})}
e
2
∑
f
(
n
)
{\displaystyle 2\sum f(n)}
.
,
∑
2
n
f
(
2
n
)
{\displaystyle \sum 2^{n}f(2^{n})}
e
2
∑
f
(
n
)
{\displaystyle 2\sum f(n)}
.
Teorema 1
A série ∑ 1 n p {\displaystyle \sum {\frac {1}{n^{p}}}} converge se p > 1 {\displaystyle p>1} e diverge se p ≤ 1 {\displaystyle p\leq 1} .
converge se
p
>
1
{\displaystyle p>1}
.
Demonstração
Se p ≤ 0 {\displaystyle p\leq 0} a série claramente diverge, já que lim n → ∞ 1 n p ≠ 0 {\displaystyle \lim _{n\rightarrow \infty }{\frac {1}{n^{p}}}\neq 0} . Se p > 0 {\displaystyle p>0} , aplicando o teste da condensação, temos:
a série claramente diverge, já que
lim
n
→
∞
1
n
p
≠
0
{\displaystyle \lim _{n\rightarrow \infty }{\frac {1}{n^{p}}}\neq 0}
. Se
p
>
0
{\displaystyle p>0}
, aplicando o teste da condensação, temos:
∑ n = 0 ∞ 2 n 1 2 n p = ∑ n = 0 ∞ 2 ( 1 − p ) n {\displaystyle \sum _{n=0}^{\infty }2^{n}{\frac {1}{2^{np}}}=\sum _{n=0}^{\infty }2^{(1-p)n}} .
.
Temos 2 1 − p < 1 {\displaystyle 2^{1-p}<1} se e somente se 1 − p < 0 {\displaystyle 1-p<0} , ou seja, p > 1 {\displaystyle p>1} . O resultado segue da convergência da série série geométrica, fazendo r = 2 1 − p {\displaystyle r=2^{1-p}} .
se e somente se
1
−
p
<
0
{\displaystyle 1-p<0}
, ou seja,
p
>
1
{\displaystyle p>1}
.Teorema 2
Se p > 1 {\displaystyle p>1} então a série ∑ n = 2 ∞ 1 n ( log n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\log {n})^{p}}}} converge. Se p ≤ 1 {\displaystyle p\leq 1} então a série diverge.
converge. Se
p
≤
1
{\displaystyle p\leq 1}
Demonstração
A monotonocidade da função logarítmica implica que log n {\displaystyle \log {n}} é crescente. Sendo assim, 1 / n log n {\displaystyle 1/n\log {n}} é decrescente, e o teste da condensação pode ser aplicado.
é crescente. Sendo assim,
1
/
n
log
n
{\displaystyle 1/n\log {n}}
é decrescente, e o teste da condensação pode ser aplicado.
∑ n = 1 ∞ 2 n 1 2 n ( log 2 n ) p = ∑ n = 1 ∞ 1 ( n log 2 ) p = 1 ( log 2 ) p ∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }2^{n}{\frac {1}{2^{n}(\log {2^{n}})^{p}}}=\sum _{n=1}^{\infty }{\frac {1}{(n\log {2})^{p}}}={\frac {1}{(\log {2})^{p}}}\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} e o resultado segue do teorema anterior.
e o resultado segue do teorema anterior.Referências
- ↑ Rudin, Walter (1976). Principles of Mathematical Analysis Terceira ed. : McGraw-Hill. p. 62. ISBN 978-0-07-054235-8
- ↑ Rudin, Walter (1976). Principles of Mathematical Analysis Terceira ed. : McGraw-Hill. p. 63. ISBN 978-0-07-054235-8