Lei de Faraday-Neumann-Lenz
Vamos mergulhar no fascinante mundo de Lei de Faraday-Neumann-Lenz, um tema que chamou a atenção de milhões de pessoas em todo o mundo. Seja pelo seu impacto na sociedade, pela sua relevância histórica ou pela sua influência na esfera cultural, Lei de Faraday-Neumann-Lenz tornou-se um tema de conversa diária. Ao longo dos anos, tem gerado interesse e debate, provocando profundas reflexões e análises sobre o seu significado e implicações nas nossas vidas. Neste artigo, exploraremos as múltiplas facetas de Lei de Faraday-Neumann-Lenz, proporcionando uma visão nova e enriquecedora que nos permitirá compreender melhor a sua importância e relevância no contexto atual.
| Artigos sobre |
| Eletromagnetismo |
|---|
 |
|
A lei de Faraday-Neumann-Lenz,[nota 1] ou lei da indução de Faraday, ou simplesmente, lei da indução eletromagnética, é uma das equações básicas do eletromagnetismo. Ela prevê como um campo magnético interage com um circuito elétrico para produzir uma força eletromotriz — um fenômeno chamado de indução eletromagnética. É a base do funcionamento de transformadores, alternadores, dínamos, indutores, e muitos tipos de motores elétricos, geradores e solenoides.[1][2]
Atribui-se a Michael Faraday a descoberta da indução eletromagnética e, por conseguinte, o nome da lei relativa a esse fenômeno. Este foi comprovado experimentalmente por Faraday diversas vezes, apesar de sua explicação limitar-se ao conceito de linhas de força. A primeira formulação matemática da lei de Faraday foi feita por Franz Ernst Neumann em 1845. Nela, a força eletromotriz produzida em um circuito, pela indução, era expressa pelo negativo da derivada do fluxo magnético com o tempo através da área delimitada por esse circuito. O sinal negativo diz respeito ao sentido da FEM – e, por conseguinte, da corrente elétrica – e pode ser expressa formalmente por meio da chamada Lei de Lenz, desenvolvida por Heinrich Lenz em 1834, que integra o corolário da lei de Faraday.
Suas aplicações são inúmeras; na prática, quase todos os equipamentos eletro-eletrônicos utilizam o fenômeno da indução, seja para produzir uma corrente contínua, como nos dínamos, ou uma corrente alternada, como nos geradores, transformadores, alternadores e indutores, todos por meio da variação no campo magnético.
A equação de Maxwell–Faraday é uma generalização da lei de Faraday, e compõe uma das equações de Maxwell. Ela descreve como a variação de um campo magnético no tempo através de um circuito em repouso produz um campo elétrico não-eletrostático que, por sua vez, produz uma corrente elétrica no circuito. O movimento relativo entre um imã e o condutor e a produção, ou não, de um campo elétrico nessa experiência levaram a uma aparente dicotomia, exercendo, por sua vez, papel fundamental no desenvolvimento da relatividade restrita por Albert Einstein em 1905.
História

A indução eletromagnética foi descoberta de forma independente por Michael Faraday em 1831 e Joseph Henry em 1832.[3] Faraday, no entanto, foi o primeiro a publicar os resultados de seus experimentos.[4] Em 29 de agosto de 1831, data da primeira demonstração experimental da indução eletromagnética feita por Faraday,[5] ele amarrou dois fios em lados opostos de um anel de ferro (ou toro, um arranjo similar a um transformador toroidal moderno). Face às recém-descobertas propriedades do eletromagnetismo, ele esperava que, quando a corrente começasse a passar em um fio, uma espécie de onda viajaria através do anel e causaria algum efeito elétrico no lado oposto. Conectou, então, um dos fios a um galvanômetro e o outro a uma bateria. Foi observada, de fato, uma corrente transiente – que ele chamou de "onda de eletricidade" – nos momentos em que conectou e desconectou o fio à bateria.[6] Esta indução ocorreu devido à mudança que houve no fluxo magnético quando a bateria foi conectada e desconectada.[7]

Faraday explicou a indução eletromagnética usando um conceito que chamou de linhas de força. No entanto, grande parte dos cientistas da época rejeitavam suas ideias teóricas, principalmente porque não havia uma formulação matemática para elas.[8] James Clerk Maxwell, contudo, usou as ideias de Faraday como a base para sua teoria eletromagnética quantitativa.[8][9] Nos estudos de Maxwell, o aspecto da variabilidade com o tempo da indução eletromagnética é expressado como uma equação diferencial, a qual Oliver Heaviside referiu-se como a lei de Faraday, embora seja diferente da versão original da lei de Faraday. A versão de Heaviside é a forma que hoje é reconhecida como parte do grupo de equações conhecido como equações de Maxwell.
A lei de Lenz, formulada por Heinrich Lenz em 1834, descreve o "fluxo através do circuito", e fornece a direção da força eletromotriz e corrente induzidas resultantes da indução eletromagnética.
Lei de Faraday-Neumann-Lenz
Enunciado qualitativo
A versão mais difundida da lei de Faraday afirma:
Esta versão da lei de Faraday é estritamente válida apenas quando o circuito fechado é um laço de fio metálico infinitamente fino,[12] e é inválida em outras circunstâncias a serem discutidas. Uma versão diferente, a equação de Maxwell–Faraday, é válida em todas as circunstâncias.
Enunciado quantitativo
A lei da indução de Faraday faz uso do fluxo magnético ΦB através de uma superfície hipotética Σ, cujo bordo é um laço de fio metálico. Uma vez que o laço pode estar se movendo com o tempo, escreve-se Σ(t) para a superfície. O fluxo magnético é definido pela integral de superfície:
- ,
onde dA é um elemento de área da superfície Σ(t), B é o campo magnético (também chamado de "densidade do fluxo magnético"), e B·dA é um produto escalar dos dois vetores (a quantidade infinitesimal de fluxo magnético). De outro modo, o fluxo magnético através do laço é proporcional ao número de linhas do fluxo magnético que passam por ele.
Quando o fluxo se modifica — devido a uma mudança do B, ou porque o laço é movido ou deformado, ou ambos — a lei da indução de Faraday afirma que o fio adquire uma FEM, ε, definida como o trabalho por unidade de carga que uma força não-eletrostática realiza quando uma carga é transportada em volta do laço.[12][13][14][nota 2] De forma equivalente, é a voltagem que seria medida ao cortar o arame para criar um circuito aberto, ligando um voltímetro às pontas.
A lei de Faraday afirma que a FEM também é dada pela taxa de variação do fluxo magnético:
- ,
onde ε é a força eletromotriz (FEM) e ΦB é o fluxo magnético. A direção da FEM é dada pela lei de Lenz.
Para um fio enrolado firmemente em uma bobina, composta de N voltas idênticas, cada uma com o mesmo ΦB, a lei da indução de Faraday afirma:[15][16]
- ,
onde N é o número de voltas do fio e ΦB é o fluxo magnético através de uma única volta.
Equação de Maxwell-Faraday
A equação de Maxwell-Faraday é uma generalização da lei de Faraday, e afirma que um campo magnético que varia com o tempo é sempre acompanhado por um campo elétrico não-conservativo que varia espacialmente, e vice-versa. A equação de Maxwell–Faraday é:
(em unidades do SI), onde é o operador rotacional e, novamente, E(r, t) é o campo elétrico e B(r, t) é o campo magnético. Tais campos podem estar em função da posição r e do tempo t.
A equação de Maxwell–Faraday é uma das quatro equações de Maxwell, tendo, portanto, um papel fundamental na teoria do eletromagnetismo clássico. Ela também pode ser escrita na forma integral pelo Teorema de Kelvin-Stokes:[17]
,
onde Σ é uma superfície limitada pelo seu bordo ∂Σ; E é o campo elétrico; B é o campo magnético; dℓ é um elemento vetorial infinitesimal de ∂Σ; dA é um elemento vetorial infinitesimal de Σ.
Ambos dℓ e dA têm uma ambiguidade de sinal; para obter o sinal correto, usa-se a regra da mão direita. Para uma superfície plana Σ, um elemento de curva positivo dℓ da curva ∂Σ é definido pela regra de mão direita como estando na direção dos dedos da mão direita quando o polegar aponta na direção do vetor normal n exterior à superfície Σ.
Demonstração
As quatro equações de Maxwell (incluindo a equação de Maxwell–Faraday), junto à lei da força de Lorentz, são suficientes para derivar tudo no eletromagnetismo clássico.[12][13] Portanto, é possível "demonstrar" a lei de Faraday partindo dessas equações.[18][19] Em uma abordagem alternativa, não mostrada aqui, porém igualmente válida, a lei de Faraday poderia ser tomada como ponto de partida e usada para "demonstrar" a equação de Maxwell–Faraday e/ou outras leis.
Esboço da demonstração da lei de Faraday partindo das equações de Maxwell e da lei da força de Lorentz. Considere a derivada em função do tempo do fluxo magnético através de um circuito fechado, possivelmente móvel, com área : A integral pode mudar em função do tempo por duas razões: o integrando pode mudar, ou a região de integração o pode. A solução geral pode ser tomada pela combinação linear dessas duas soluções particulares, portanto:
onde t0 é qualquer tempo fixo dado. O primeiro termo do lado direito da equação pode ser reescrito usando a forma integral da equação de Maxwell–Faraday:
Área definida pelo elemento vetorial dℓ da curva ∂Σ, no tempo dt, quando se desloca com velocidade v. Em seguida, analisamos o segundo termo do lado direito da equação:
Esta é considerada a parte mais difícil da demonstração; mais detalhes e abordagens alternativas podem ser encontradas nas referências.[18][19][20] Conforme o circuito move e/ou se deforma, ele define uma superfície. Analisando o fluxo magnético através da superfície total que delimita um volume tido após esse deslocamento, notamos que o fluxo através das "tampas" delimitadas pelo circuito é igual; logo, o fluxo que contribui para a derivada no tempo corresponde apenas àquele através da área lateral desse volume (aqui, usamos implicitamente a lei de Gauss para o magnetismo). À medida que uma parte do circuito move-se com velocidade v por um período de tempo , ela define um vetor área . Assim, a mudança do fluxo magnético com o tempo através do circuito é:
Portanto:
onde v é a velocidade em um ponto do circuito de trajetória .
Juntando as equações,
A FEM é definida como a energia disponível por unidade de carga que viaja uma vez pelo circuito. Portanto, pela lei da força de Lorentz,
Recombinando,
Contraexemplos
-
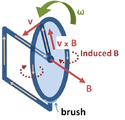
Gerador unipolar ou disco de Faraday: O disco gira com uma frequência angular ω, movendo o raio condutor circularmente na presença de um campo magnético estacionário B. A força magnética de Lorentz v × B conduz a corrente ao longo do raio condutor, em seguida pelo aro condutor, e, deste, à ligação inferior para um circuito reto até a haste que sustenta o disco. Este dispositivo gera uma FEM e uma corrente, embora o formato do "circuito" seja constante e, portanto, o fluxo magnético não muda com o tempo.
-
Um contraexemplo da lei de Faraday quando extrapolada sua interpretação. Um fio (linhas vermelhas) se conecta a duas placas de metal que se encostam, formando um circuito. Todo o sistema está sujeito a um campo magnético uniforme, com normal exterior à página. Se a palavra "circuito" é interpretada como o "percurso primário da passagem da corrente", logo o fluxo magnético através do "circuito" muda dramaticamente quando as placas são rotacionadas; no entanto, a FEM permanece próxima de zero, o que contradiz a lei de Faraday.
Embora a lei de Faraday seja válida para circuitos de fio infinitamente fino, ela pode fornecer um resultado errado caso seja ingenuamente extrapolada para outros contextos.[12] Um exemplo é o gerador unipolar: um disco metálico girando na presença de um campo magnético homogêneo gera uma FEM de corrente contínua. Na lei de Faraday, a FEM é dada pela derivada do fluxo no tempo; logo, uma FEM contínua só é possível caso o fluxo magnético esteja aumentando. Porém, no gerador, o campo magnético é constante e o disco permanece na mesma posição, então, o fluxo magnético não aumenta. Portanto, esse exemplo não pode ser analisado diretamente pela lei de Faraday.
Outro exemplo, como exposto por Richard Feynman,[12] apresenta uma mudança dramática no fluxo através do circuito, no entanto, a FEM permanece arbitrariamente pequena. Veja a figura e legenda acima à direita.
Em ambos os exemplos, as mudanças no percurso da corrente são diferentes do movimento do material que compõe o circuito. Os elétrons em um material tendem a seguir o movimento dos átomos que constituem o material, devido à dispersão na massa e o confinamento da função trabalho nas bordas. Por conseguinte, a FEM relativa ao movimento é gerada quando os átomos do material movem-se através de um campo magnético, arrastando os elétrons com ela, sujeitando-os, assim, à força de Lorentz. No gerador unipolar, os átomos do material movem-se, embora a geometria do circuito como um todo permaneça a mesma. No segundo exemplo, os átomos do material são praticamente estacionários, embora a geometria do circuito como um todo mude dramaticamente. Por outro lado, a lei de Faraday sempre é verdadeira para um fio suficientemente fino, pois a mudança na geometria do circuito é sempre diretamente proporcional ao movimento dos átomos do material.
Embora a lei de Faraday não seja válida em todas as situações, a equação de Maxwell–Faraday e a lei da força de Lorentz são sempre corretas e podem ser sempre usadas diretamente.[12]
A lei de Faraday e a relatividade
Dois fenômenos
Alguns físicos observaram que a lei de Faraday é uma única equação que descreve dois fenômenos diferentes: uma FEM gerada pela força magnética em um circuito móvel, e uma FEM gerada por uma força elétrica devido a uma mudança no campo magnético (dada a equação de Maxwell–Faraday). James Clerk Maxwell chamou atenção para esse fato em On Physical Lines of Force de 1861. Na segunda metade da Parte II do livro, Maxwell fornece uma explicação física separada para cada um dos dois fenômenos.
Em muitos livros modernos, é feita uma referência a esses dois aspectos da indução eletromagnética.[21] Em The Feynman Lectures on Physics, Richard Feynman afirma que a "regra do fluxo" (terminologia por ele usada para referir-se à lei que relaciona o fluxo magnético à FEM) pode ser aplicada tanto no caso em que o fluxo muda porque o campo muda quanto quando o circuito se move, ou ambos. Ele observa que "não se sabe de nenhum outro lugar na física onde um princípio geral tão simples e preciso requer, para seu entendimento real, uma análise em termos de dois fenômenos diferentes".[12]
Visões de Einstein
A reflexão acerca dessa aparente dicotomia foi uma das principais razões que levaram Albert Einstein a desenvolver a relatividade restrita:
Sabe-se que, se tentarmos aplicar a eletrodinâmica de Maxwell, como é usualmente conhecida na atualidade, a corpos móveis, somos levados a assimetrias que não concordam com fenômenos observados. Pensemos na ação mútua entre um imã e um condutor.O fenômeno observado neste caso depende apenas do movimento relativo do condutor e do imã, enquanto que, de acordo com a concepção habitual, uma distinção deve ser feita entre os casos nos quais ou um ou outro dos corpos está em movimento. Caso, por exemplo, o imã mova-se e o condutor esteja em repouso, logo, um campo elétrico com uma certa energia definida é produzido nas proximidades do imã, que excita uma corrente nas partes do campo nas quais o condutor se situa.
Porém, se o imã estiver estacionário e o condutor em movimento, nenhum campo elétrico é produzido nas proximidades do imã, contudo, uma força eletromotriz, para qual, em si, não há energia correspondente, é produzida no condutor; ela faz surgir uma corrente elétrica de mesma intensidade e caminho àquela produzida pelas forças elétricas no caso anterior, assumindo, claro, a igualdade do movimento relativo nos dois casos discutidos.
Exemplos dessa natureza, tal como as tentativas frustradas de justificar o movimento da Terra relativo ao "meio lumnífero", sugerem que, não apenas na mecânica, mas também na eletrodinâmica, nenhuma propriedade de fatos observados correspondem à ideia de repouso absoluto.
Aplicações
As aplicações da lei de Faraday são inúmeras, podendo-se citar: indutores, alternadores, dínamos e transformadores.[23] Praticamente todos os equipamentos eletros-eletrônicos usam o fenômeno de indução, seja com indutores em circuitos ou em transformadores para utilizar vários níveis de tensão.
Transformador
Vamos usar como exemplo um transformador ideal. Um transformador ideal consiste de um núcleo que contém completamente o fluxo magnético dentro dele e duas bobinas: uma que chega com a tensão e corrente vindas de um gerador e o outro lado que vai ser usado em algum circuito, uma tomada por exemplo.[24]
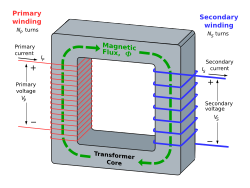
Dado o número de voltas da bobina 1 e o número de voltas da bobina 2. Temos então:
Como a tensão de entrada é conhecida e o fluxo magnético é igual nas duas bobinas:
E a razão entre as tensões depende somente da razão entre o número de voltas das bobinas:
Gerador
Como visto antes, o processo regido pela Lei de Faraday-Neumann-Lenz não discrimina entre condutor ou ímã se movendo.
O fluxo de um campo magnético uniforme passando por uma bobina fina pode ser escrito como:[25]
Onde é o ângulo entre o campo e a normal da área orientada da bobina. Se a bobina está girando temos:
- .
Calculamos a FEM (força eletromotriz) então como:
Esse tipo de gerador é um exemplo de modelo de gerador que fornece a corrente alternada que é usada no cotidiano
Ver também
Notas
- ↑ Devido à importância de físicos como Franz Ernst Neumann, Joseph Henry e Heinrich Lenz na formulação da lei, seu nome pode ser tido também pela aglutinação de seus sobrenomes ao de Faraday. Portanto, também pode ser conhecida como lei de Faraday-Lenz, lei de Faraday-Neumann e lei de Faraday-Henry. É referida apenas como lei de Faraday no decorrer do artigo, por simplicidade.
- ↑ Repara-se que diferentes textos podem fornecer diferentes definições. O conjunto de equações usado em todo o texto foi escolhido a fim de ser compatível com a teoria da relatividade restrita.
- ↑ Tradução livre do texto de 1920, da tradução inglesa, que dizia: "It is well known that if we attempt to apply Maxwell's electrodynamics, as conceived at the present time, to moving bodies, we are led to assymetry which does not agree with observed phenomena. Let us think of the mutual action between a magnet and a conductor. The observed phenomena in this case depend only on the relative motion of the conductor and the magnet, while according to the usual conception, a distinction must be made between the cases where the one or the other of the bodies is in motion. If, for example, the magnet moves and the conductor is at rest, then an electric field of certain energy-value is produced in the neighbourhood of the magnet, which excites a current in those parts of the field where a conductor exists. But if the magnet be at rest and the conductor be set in motion, no electric field is produced in the neighbourhood of the magnet, but an electromotive force which corresponds to no energy in itself is produced in the conductor ; this causes an electric current of the same magnitude and the same career as the electric force, it being of course assumed that the relative motion in both of these cases is the same. Examples of a similar kind such as the unsuccessful attempt to substantiate the motion of the earth relative to the "Light-medium" lead us to the supposition that not only in mechanics, but also in electrodynamics, no properties of observed facts correspond to a concept of absolute rest (…)"
Referências
- ↑ Sadiku, Matthew N. O. (2007). Elements of Electromagnetism (em inglês) 4ª ed. Nova Iorque/Oxford: Oxford University Press. p. 386. 765 páginas. ISBN 0-19-530048-3
- ↑ «Applications of electromagnetic induction» (em inglês). Universidade de Boston. 22 de julho de 1999. Consultado em 1 de janeiro de 2015
- ↑ Steven Errede (2007). «A Brief History of The Development of Classical Electrodynamics» (em inglês). Universidade de Illinois. Consultado em 1 de janeiro de 2015
- ↑ Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (em inglês) 5ª ed. : Pearson: Prentice Hall. p. 255. ISBN 0-13-241326-4}
- ↑ Day, Peter (1999). The philosopher's tree. A selection of Michael Faraday's writings (em inglês). : CRC Press. p. 71. 211 páginas. ISBN 978-0-7503-0570-9. Consultado em 1 de janeiro de 2015
- ↑ L. Pearce Williams. Michael Faraday. p. 182-3
- ↑ L. Pearce Williams. Michael Faraday. p. 181-5
- ↑ a b L. Pearce Williams. Michael Faraday. p. 510
- ↑ Maxwell, James Clerk (1904). A Treatise on Electricity and Magnetism (em inglês). 2 3ª ed. : Oxford University Press. p. 178-9 e 189
- ↑ "Faraday's Law, which states that the electromotive force around a closed path is equal to the negative of the time rate of change of magnetic flux enclosed by the path" Jordan, Edward; Balmain, Keith G. (1968). Electromagnetic Waves and Radiating Systems 2ª ed. : Prentice-Hall. p. 100
- ↑ "The magnetic flux is that flux which passes through any and every surface whose perimeter is the closed path"Hayt, William (1989). Engineering Electromagnetics 5ª ed. : McGraw-Hill. p. 312. ISBN 0-07-027406-1
- ↑ a b c d e f g Feynman, Richard Phillips; LEIGHTON R. B. e SANDS M. L. (2006). The Feynman Lectures on Physics. Mainly Electromagnetism and Matter (em inglês). 2. Uma versão online pode ser encontrada nesta página do Instituto de Tecnologia da Califórnia. São Francisco (Califórnia) (EUA): Pearson/Addison-Wesley. p. 17-2. ISBN 0-8053-9049-9
- ↑ a b Griffiths, David J. (1999). Introduction to Electrodynamics 3ª ed. Upper Saddle River NJ: Prentice Hall. pp. 301–303. ISBN 0-13-805326-X
- ↑ Tipler and Mosca, Physics for Scientists and Engineers, p795, google books link
- ↑ Essential Principles of Physics, P.M. Whelan, M.J. Hodgeson, 2nd Edition, 1978, John Murray, ISBN 0-7195-3382-1
- ↑ Nave, Carl R. «Faraday's Law». HyperPhysics. Universidade do Estado da Geórgia. Consultado em 29 de agosto de 2011
- ↑ Roger F Harrington (2003). Introduction to electromagnetic engineering. Mineola, NY: Dover Publications. p. 56. ISBN 0-486-43241-6
- ↑ a b Davison, Mark E. (1 de maio de 1973). «A Simple Proof that the Lorentz Force, Law Implied Faraday's Law of Induction, when B is Time Independent». American Journal of Physics (5): 713–713. ISSN 0002-9505. doi:10.1119/1.1987339. Consultado em 23 de novembro de 2022
- ↑ a b Krey, Uwe; Owen, Anthony (14 de agosto de 2007). Basic Theoretical Physics: A Concise Overview (em inglês). : Springer Science & Business Media
- ↑ K. Simonyi, Theoretische Elektrotechnik, 5th edition, VEB Deutscher Verlag der Wissenschaften, Berlin 1973, equation 20, page 47
- ↑ Griffiths, David J. (1999). Introduction to Electrodynamics (em inglês). Repare que a lei que relaciona o fluxo magnético à FEM, chamada de lei de Faraday neste artigo, é chamada, pela terminologia de Griffiths, de "regra do fluxo universal". Griffiths usa o termo "lei de Faraday", por outro lado, para se referir ao que o artigo chama de "equação de Maxwell-Faraday". 3 ed. Upper Saddle River, Nova Jérsei: Prentice Hall. p. 301-3. ISBN 0-13-805326-X
- ↑ EINSTEIN, Albert; MINKOWSKI, Hermann; SAHA, Meghnad; BOSE, Satyendranath (1920). The Principle of Relativity: Original Papers by A. Einstein and H. Minkowski (em inglês). Baseado na versão original em alemão: EINSTEIN, Albert (1905), "Zur Elektrodynamik bewegter Körper", Annalen der Physik 322 (10): 891–921. : Universidade de Calcutá. 34 páginas
- ↑ Young, Hugh D.; Freedman, Roger A. (2016). Física III - Eletromagnetismo 14 ed. São Paulo: Pearson. p. 304-399. ISBN 978-85-430-1591-0
- ↑ «Transformador ideal». dsee.fee.unicamp.br. Consultado em 9 de janeiro de 2012. Arquivado do original em 9 de janeiro de 2012
- ↑ Nussenzveig, H.M., Curso de Física básica – vol 3 1ª Ed pg171